| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Kurvenanpassung Kurvenanpassung  Extrapolation Extrapolation |
|||
| Siehe auch: Generalisierung und Overtraining, Neuronale Netze und Extrapolation, Interpolation | |||
| Search the VIAS Library | Index | |||
|
ExtrapolationAuthor: Hans Lohninger
Bei der Kurvenanpassung muss man grundsätzlich zwei Bereiche unterscheiden: den Bereich der Interpolation und den der Extrapolation.
Setzt man eine einfache Regressionsgerade als Modell ein, so werden die extrapolierten Werte über einen weiteren Bereich der x-Werte gültig sein, als wenn man ein Spline oder gar ein neuronales Netz verwendet.
|
|||
Home  Bivariate Daten Bivariate Daten  Kurvenanpassung Kurvenanpassung  Extrapolation Extrapolation |
|||
Last Update: 2012-10-12


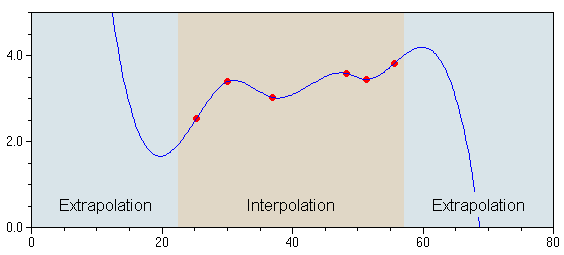
 Die nebenstehende Abbildung vergleicht das Extrapolationsverhalten eines neuronalen Netzes mit dem einer einfachen linearen Regression.
Die nebenstehende Abbildung vergleicht das Extrapolationsverhalten eines neuronalen Netzes mit dem einer einfachen linearen Regression.