Einseitige und zweiseitige Tests

Author: Hans Lohninger

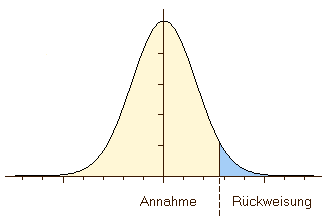
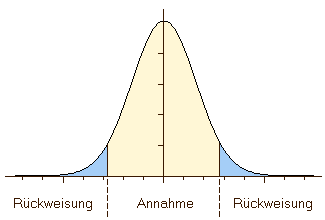
Da das Treffen einer Entscheidung - statistisch gesprochen - die Auswahl eines Grenzwerts auf einer eindimensionalen Skala (d.h. auf der Argumentachse des Wahrscheinlichkeitsdichtediagramms) ist, müssen wir zwischen zwei Fällen unterscheiden: Zum einen sollte man sich fragen, ob die Eigenschaft über oder unter dem vorgegebenen Grenzwert liegt (linke Grafik); in diesem Fall müssen wir einen einseitigen Test anwenden. Zum anderen kann es von Interesse sein, zu bestimmen, ob eine Eigenschaft innerhalb gewisser Grenzen liegt. Diese Frage macht es notwendig, zwei Grenzen zu setzen und nach der Wahrscheinlichkeit zu fragen, mit der ein Ereignis innerhalb oder außerhalb dieser Grenzen liegt (rechte Grafik). In diesem Fall müssen wir einen zweiseitigen Test anwenden.

Beispiel

Übersteigt die Eisenkonzentration eines Eisenerzes 30%? [einseitiger Test] Ist die bestellte Pizza vom Pizzaservice gut durchgebacken (sie kann roh, verbrannt oder gut durchgebacken sein)? [zweiseitiger Test]

Allgemein gesagt, bauen wir die Entscheidung auf dem Wert einer Testgröße auf, z.B. dem Durchschnitt der Eisenkonzentration oder der Qualität einer Pizza. Diese Testgröße kann der Mittelwert einer Eigenschaft sein, ihre Varianz, oder auch eine beliebige andere Größe. Die Menge aller möglichen Werte dieser Testgröße wird als Datenraum bezeichnet. Unsere Entscheidung teilt den Datenraum in zwei sich gegenseitig ausschließende Bereiche: den Annahmebereich und den Ablehnungs- oder Rückweisungsbereich. Wenn Sie die oben stehenden Grafiken betrachten, sehen Sie sofort, warum manche Tests einseitig und andere zweiseitig genannt werden. Einseitige Tests haben nur einen Ablehnungsbereich, d.h. sie überprüfen, ob der entsprechende Parameter größer (oder kleiner) als der gegebene Wert ist. Zweiseitige Tests werden angewendet, wenn ein Parameter auf Gleichwertigkeit mit einem bestimmten Wert überprüft werden soll. Abweichungen in beide Richtungen von diesem Wert werden verworfen.