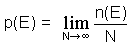Wahrscheinlichkeit - Einführung

Author: Hans Lohninger

Wahrscheinlichkeit wird oft als Synonym für die Begriffe "Zufall", "Risiko" oder "Möglichkeit" gebraucht. Die Wahrscheinlichkeit sagt aus, mit welcher Erwartung ein Ereignis eintritt. Wie hoch sind die Chancen, in der Lotterie zu gewinnen? Wie groß ist die Möglichkeit, dass wir von einem Hurrikan erfasst werden? Wie hoch ist das Risiko einer Investition? Die Wahrscheinlichkeit eines Ereignisses ist oft sehr schwer zu beurteilen und einzuschätzen. Dennoch kann die Wahrscheinlichkeit in einigen einfachen und sehr genau definierten Situationen direkt angegeben werden.

Wenn alle Ergebnisse eines Experiments gleich wahrscheinlich sind und wir den Merkmalsraum kennen, können wir jeder Beobachtung eine Wahrscheinlichkeit von 1/N zuordnen, wobei N die Anzahl der Beobachtungen ist. Wir können zu diesem Schluss kommen, da nur eines der N Ergebnisse für jedes Experiment möglich ist.

Beispiel 1:

Wenn wir eine Münze werfen, wissen wir, dass es zwei mögliche Ergebnisse (den Merkmalsraum) gibt. Daraus können wir folgern, dass wir eine 50 : 50 Chance haben, Kopf zu werfen; es sei denn, wir vermuten, dass die Münze nicht ausgewogen ist.

Für komplexere Experimente ist die Zahl der Beobachtungen oft zu groß, um sie explizit aufzulisten. Daher benötigen wir ausgeklügelte Zählregeln, um die Anzahl der möglichen Beobachtungen zu bestimmen.

Beispiel 2:

Wie hoch ist die Wahrscheinlichkeit, mit 3 Münzen genau zwei Mal Kopf zu werfen? Der Stichprobenraum ist: KKK ZZK ZKK ZKZ KZK ZZK KKZ ZZZ Daher ist die Wahrscheinlichkeit, mit 3 Münzen genau zwei Mal Kopf zu werfen, 3/8.

Beispiel 3:

Wie hoch ist die Wahrscheinlichkeit, mit 5 Münzen genau drei Mal Kopf zu werfen? Die möglichen Kombinationen drei Mal die Kopfseite zu bekommen, sind: ZZKKK KZZKK KKZZK KKKZZ ZKZKK KZKZK KKZKZ ZKKZK KZKKZ ZKKKZ. Um die Wahrscheinlichkeit zu berechnen, müssen wir alle möglichen Ergebnisse kennen. Es gibt 32 davon. Diese Zahl erhalten wir aus folgender Überlegung: Anzahl der Köpfe Anzahl der möglichen Ergebnisse mit der genannten Anzahl an Köpfen Bemerkung 0 1 Es gibt nur eine Möglichkeit. 1 5 Der Kopf kann an jeder der fünf Positionen sein. 2 10 Wenn wir K und Z in der oberen Liste austauschen. 3 10 Wurde oben aufgelistet. 4 5 Das ist dasselbe wie eine Zahl. 5 1 Es gibt nur eine Möglichkeit. Summe 32

Wenn wir uns nicht auf die Annahme verlassen können, dass alle Beobachtungen gleich wahrscheinlich sind, müssen wir die Wahrscheinlichkeit mit der ein Ereignis eintritt, experimentell bestimmen. Wir führen eine große Zahl N an Experimenten durch und zählen, wie oft jede Beobachtung eintritt. Das Verhältnis der Anzahl des Auftretens einer bestimmten Beobachtung zur Gesamtzahl der Experimente wird als relative Häufigkeit bezeichnet.

Der Wahrscheinlichkeit wird die relative Häufigkeit des Auftretens einer Beobachtung in einer langen Serie von Wiederholungen des Experiments zugewiesen. Das basiert auf dem Axiom "des Gesetzes der großen Zahlen", das aussagt, dass sich die relative Häufigkeit der wahren (theoretischen) Wahrscheinlichkeit nähert, wenn das Experiment mehrmals wiederholt wird.

n(E) gibt an, wie oft das Ereignis E aus einer Gesamtmenge von N Experimenten stattgefunden hat. Aus dieser Definition sehen wir, dass die Wahrscheinlichkeit eine Zahl zwischen 0 und 1 ist. Wenn die Wahrscheinlichkeit 1 ist, dann wissen wir, dass das bestimmte Ergebnis sicher ist.