| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Zeitserien Zeitserien  Trends Trends |
|
| Siehe auch: Zeitreihen - Vorhersage | |
| Search the VIAS Library | Index | |
|
Zeitreihen - TrendsAuthor: Hans Lohninger
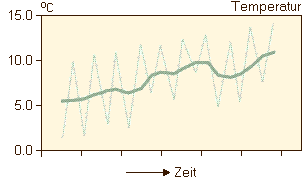
Misst man die Temperatur zweimal am Tag, könnte die resultierende Zeitreihe etwa wie folgt aussehen:
Dabei lassen sich zwei typische Phänomene beobachten: ein Aufwärtstrend und ein täglicher Zyklus. Je nach Anwendung kann es nötig sein, vor der Modellbildung sowohl den Trend als auch das zyklische Muster aus dem Datensatz zu entfernen, da viele (typische) Modelle stationäre Zeitreihen benötigen. Wenn sich die Charakteristiken einer Zeitreihe (zum Beispiel der Mittelwert und die Varianz) zu verschiedenen Zeitpunkten voneinander unterscheiden, ist die Zeitreihe nicht stationär. Nach dem Entfernen des Trends der Zeitreihe in unserem Beispiel, sieht die Zeitreihe so aus:
Nachdem die täglichen Zyklen, die durch die zwei Messungen pro Tag entstanden sind, gemittelt wurden, erhält man folgende Zeitreihe:
Zuletzt erhält man nach Entfernen des Trends und der Zyklen diese Serie:
Nach der Bereinigung kann man die Eigenschaften der resultierenden
Zeitreihe überprüfen. Falls sie wirklich stationär ist, bietet sie die
Grundlage für die Erstellung eines Modells. Um nun zukünftige Werte
vorauszusagen, muss das Ergebnis, das man bei der Verwendung des Modells erhält,
transformiert werden, damit der Trend und der tägliche Zyklus wieder
miteinbezogen werden.
|
|
Home  Bivariate Daten Bivariate Daten  Zeitserien Zeitserien  Trends Trends |
|
Last Update: 2012-10-08