| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Optimierung Optimierung  Responsefunktion Responsefunktion |
|
| Siehe auch: Phasenraum, Visualisierung der Response-Funktion | |
| Search the VIAS Library | Index | |
|
Optimierungsmethoden - Response-FunktionAuthor: Hans Lohninger
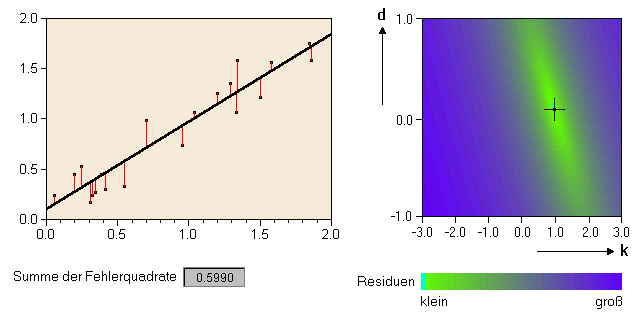
Um ein vorgegebenes Problem optimieren zu können, muss eine Response-Funktion ermittelt werden, die den Zusammenhang zwischen der unabhängigen Variablen und dem "Ziel" der Optimierung festlegt. Die Response-Funktion wird manchmal auch als Zielfunktion bezeichnet. Viele Probleme in der statistischen Analyse können als Lösung eines Optimierungsproblems neu formuliert werden. Ein einfaches Beispiel soll das zeigen: Es liegt ein Satz von zweidimensionalen Daten vor; es ist notwendig, eine Gerade an die Daten anzupassen. Mathematisch kann das Modell beschrieben werden durch y = kx + d, wobei y die Variable ist, die vom Modell vorausgesagt wird, und x die
Eingabedaten repräsentiert. k und d sind die Parameter, die gefunden (oder
optimiert) werden müssen. Wir können daher eine Response-Funktion festlegen, die
die Summe der Residuenquadrate berechnet. Die beste Anpassung minimiert die
Response-Funktion. In der linken Grafik sehen Sie eine Gerade, die an die
vorgegebenen Daten am besten angepasst ist. In der rechten Grafik sehen Sie eine
Darstellung des Phasenraums der Response-Funktion.
Klicken Sie auf das Bild, um mit dem Konzept vertraut zu werden.
|
|
Home  Multivariate Daten Multivariate Daten  Optimierung Optimierung  Responsefunktion Responsefunktion |
|
Last Update: 2012-10-08