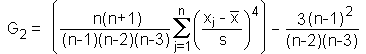Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.


Home Univariate Data Moments of a Distribution Kurtosis
See also: skewness, moments of a distribution 

Kurtosis

The kurtosis (or excess)  measures the relative flatness of a distribution (as compared to the normal distribution, which shows a kurtosis of zero). A positive kurtosis indicates a tapering distribution (also called leptokurtic distribution), whereas a negative kurtosis indicates a flat distribution (platykurtic distribution). The kurtosis is defined by the following formula:

This equation of the kurtosis is valid for a sample and is a biased estimator of the kurtosis of the population. In order to estimate the kurtosis of the population you have to use the following formula:

Below you find two examples of distributions with different kurtosis.


1 Note that the kurtosis is sometimes defined by another formula, omitting the term "-3" in the formula above. In this case a normal distribution would yield a kurtosis of 3.

Last Update: 2009-Mär-28