| Definition |
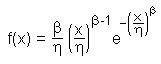
With β=1 the Weibull distribution becomes the exponential distribution (which means that the exponential distribution can be applied to problems having a constant failure rate, while the Weibull distribution can handle situations with increasing or falling failure rates, as well). |
| Graphic Representation |
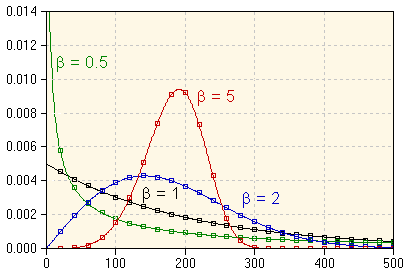 The figure at the right shows the Weibull distribution for various β value, holding η constant at η=200.
The figure at the right shows the Weibull distribution for various β value, holding η constant at η=200.
|
| Applications |
The Weibull distribution occurs mainly when investigating the mean time to failure of materials.
|
| Mean |
μ = ηΓ(1+1/β) |
| Variance |
σ2 = η2[Γ(1+2/β) - Γ2(1+1/β)] |


 Univariate Data
Univariate Data  Distributions
Distributions  Common Distributons
Common Distributons  Continuous Distributions
Continuous Distributions  Weibull Distribution
Weibull Distribution Univariate Data
Univariate Data  Distributions
Distributions  Common Distributons
Common Distributons  Continuous Distributions
Continuous Distributions  Weibull Distribution
Weibull Distribution

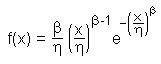
 The figure at the right shows the Weibull distribution for various β value, holding η constant at η=200.
The figure at the right shows the Weibull distribution for various β value, holding η constant at η=200.