| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Multivariate Data Multivariate Data  Basic Knowledge Basic Knowledge  Distance and Similarity Measures Distance and Similarity Measures |
|
| See also: Cluster Analysis, Distance Matrix | |
Distance and Similarity MeasuresDistances between objects in multidimensional space form the basis for many multivariate methods of data analysis. Using a different method for calculating the distances may influence the results of a method considerably. Similarity of objects and distances between them are closely related and are often confused. While the term distance is used more precisely in a mathematical sense, the particular meaning of the term similarity often depends on the circumstances and its field of application. In general, the distance dij between any two points in n-dimensional space may be calculated by the equation given by Minkowski: 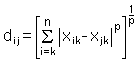 with k being the index of the coordinates, and p determining the type of distance. There are three special cases of the Minkowski distance:
The Mahalanobis distance is related to the Euclidean distance, and results in the same values for uncorrelated and standardized data. It can easily be calculated by including the inverse covariance matrix into the distance computations:
Another distance measure, which is rather a measure for the similarity
between two objects, has been proposed by Jaccard
with (x.y) being the inner product of the two vectors x, and y. Note that the Jaccard coefficient equals 1.0 for objects with zero distance. Furthermore, the Tanimoto coefficient can be appied to binary data, as well: T = Nxy / (Nx + Ny - Nxy)
with Nx, Ny.... number of 1-bits in the vectors x and y, and
|
|
Home  Multivariate Data Multivariate Data  Basic Knowledge Basic Knowledge  Distance and Similarity Measures Distance and Similarity Measures |
|


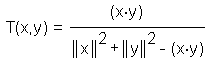 ,
,